CTO 室の恩田です。
今回は GitHub Copilot Enterprise を評価してみて、現時点ではまだ採用しないことを決めた、というお話をご紹介したいと思います。
きっかけ
とあるエンジニアが Slack で自身の times チャネルに時雨堂さんの GitHub Copilot Enterprise のススメという記事を投稿したことが発端でした。特に感想はなく URL に 👀 だけが添えられていたので、後で見るぐらいのメモだったんだと思います。
それを見かけた別のエンジニアが技術雑談チャネルにその投稿を共有して、これは凄そうと話題を向けたところ、CTO の「評価してみる?」の一言で、有志が集って評価プロジェクトが始まりました。
雑談チャネルできっかけとなる投稿が共有されてから、30分足らずの出来事でした(笑)。
この話題が出たのは金曜日でしたが、週明け早々に稟議を終え、火曜日の朝にアップグレードが完了しました。 GitHub Team から GitHub Enterprise Cloud に、Copilot Business から Copilot Enterprise への変更です。
そうして評価プロジェクトが動きはじめました。
評価にあたって
Copilot Enterprise が有効になったことを確認したあと、集った有志がどう評価を進めようか話しはじめたところで、CTO からレビューしてちゃんと意思決定しようね、との補足をもらいました。
その要旨は次の二点です。
- 会社で支払うライセンス管理は、ほとんど使ってないのにとりあえずもらっておくなど、なあなあになりがち
- 評価は定性的でよい、インパクトのあるユースケースがどれだけ見つかるかが重要
個人的には、コストに見合う価値をどう定量化するかという観点でばかり考えていたので、後者の指摘には新鮮な視点をもらえたように思います。 定量化を前提にすると評価プロセスが重たく固定的になってしまい、様々な視点からの素早い意思決定には繋がらなかったことでしょう。
結果、プロジェクトに集まったメンバーが各自の興味のある観点で分担して、どういうユースケースが実現できると開発体験にインパクトを与えられるか、で評価することになりました。
いくつか抜粋すると、
- ドキュメントを集約する場として knowledge bases は Confluence からの移行に値するか?
- レガシーコードの理解にあたり認知負荷をどれぐらい軽減してくれるか?
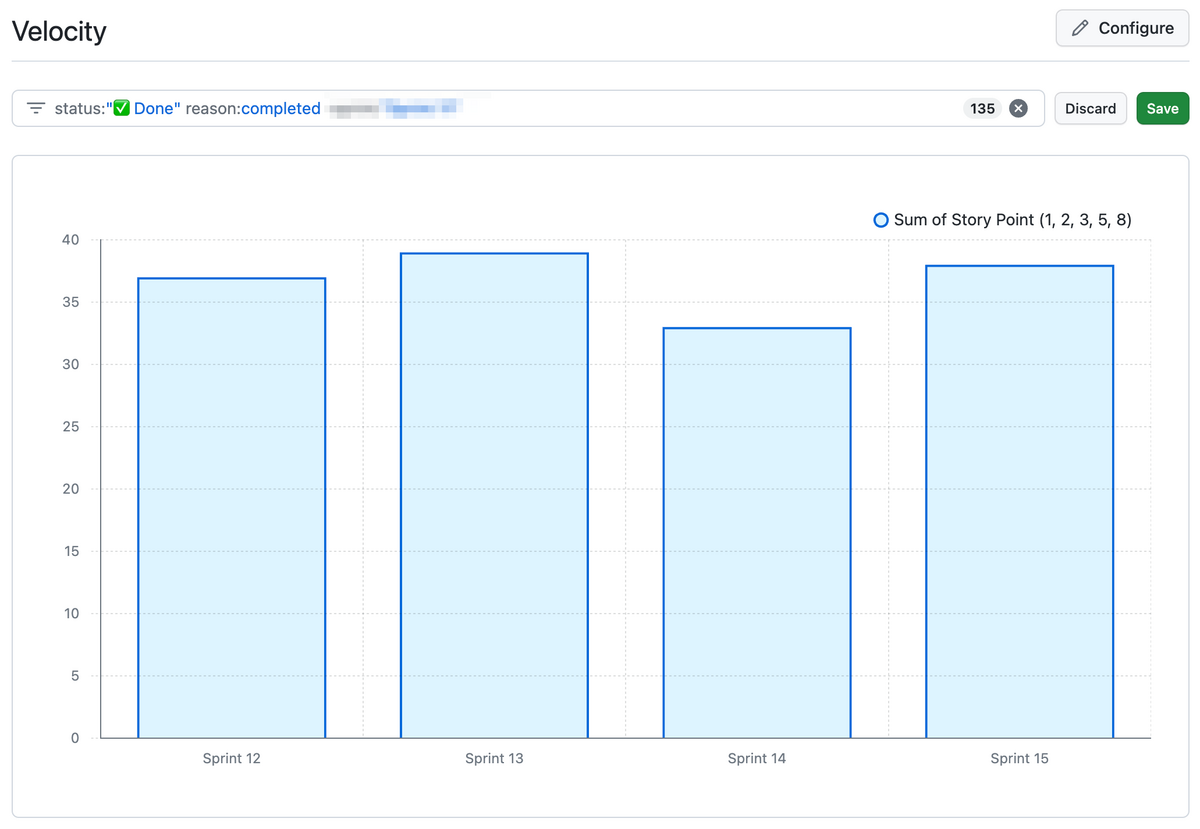
- PR サマリーの自動生成で開発プロセスがどの程度改善されるか?
といった観点になります。
評価
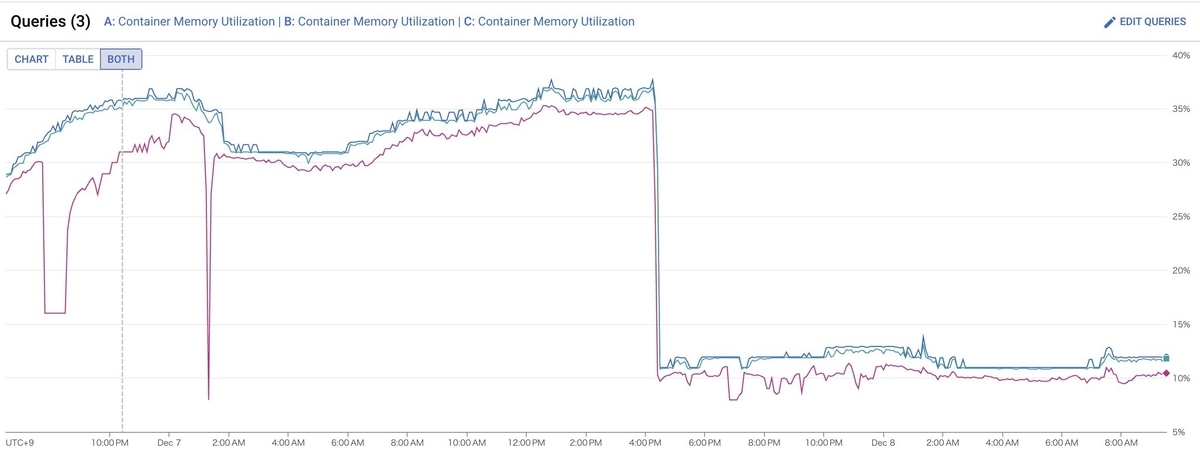
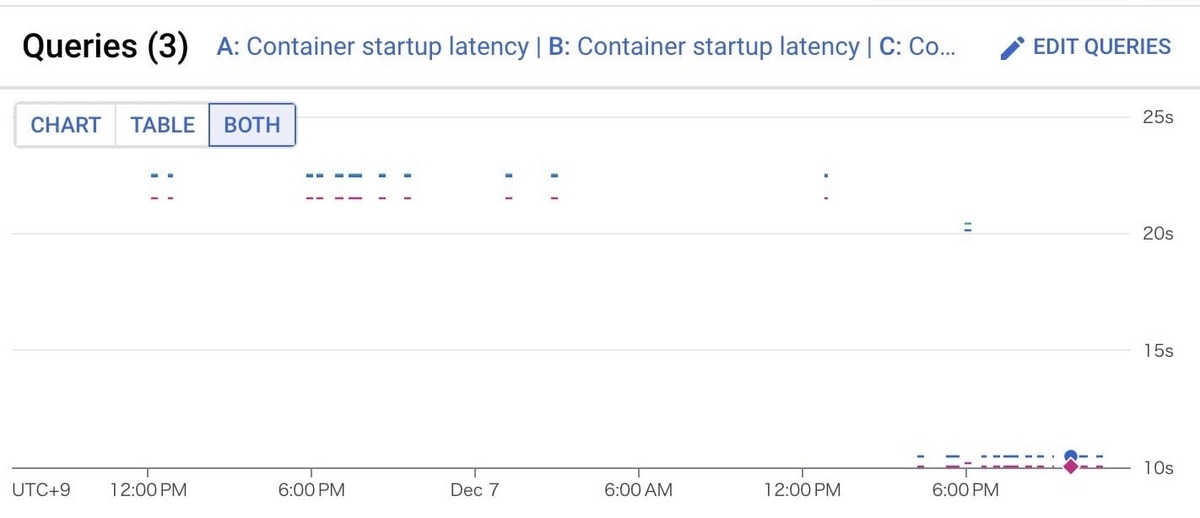
冒頭でお伝えしている通り、2024年4月現在、一休のコードベースやドキュメントを学習させた限りにおいては、GitHub Copilot Enterprise は時期尚早という結論になりました。
ここでは評価していく中で、具体的にどんなことがわかったのかをご紹介したいと思います。
knowledge bases は使えるか?
もともとプラットフォームエンジニアリングの文脈で、開発者の認知負荷を軽減させるために、ドキュメントをどうしていくかという議論が少し前からありました。
knowledge bases は2024年4月現在 GitHub リポジトリ内の markdown ファイルのみを学習します。 Copilot Enterprise を導入することになると、ドキュメントを今後は GitHub リポジトリで管理していく必要があります。
一休では現在、多くのチームが Confluence を使ってドキュメントを管理しています。
非エンジニアにとっても扱いやすく、階層的に情報を整理することができ、世界的に広く利用されているナレッジマネジメントサービスです。 特にドキュメントを同時編集したり、リアルタイムでインラインコメントを入れる機能は、一休でもミーティングの場で活用されています。
そういった現在享受している Confluence の良い点を失ってでも、なお余りある価値を Copilot Enterprise がもたらしてくれるのかが焦点でした。
上述の通り、knowledge bases にインデックスさせるデータは markdown ファイルで構成された GitHub リポジトリとして用意する必要があります。そこで、スペースを一括して markdown に出力する Confluence プラグインを導入し、それを使って knowledge bases 用のリポジトリをいくつか作成しました。
その上で、様々な質問で評価してみましたが、概念の学習がまだまだ限定的であるように感じられました。
ひとつ具体例を紹介したいと思います。
一休レストランは現在3バージョン存在します。
オリジナルの一休レストランは restaurant というリポジトリで作られました。 リニューアル時に restaurant2 が作られ、それ以後、オリジナルは restaurant1 や略して res1 と呼ばれるようになりました。
今回 knowledge bases に取り込んだドキュメントにも restaurant1 や res1 という記述が多数あります。 にも関わらず、res1 などのキーワードを含めた検索では、オリジナルのリポジトリである restaurant に関する回答が返されることはほぼありませんでした。 数字の有無が影響しているのか、restaurant2 に関する情報ばかりが要約されて返ってくることが多かったです。
他にも LLM でよく言われているように、knowledge bases においても、日本語で学習させたにも関わらず、英語で質問した方がより優れた回答になる傾向が見られました。
レガシーコードの理解にあたり認知負荷をどれぐらい軽減してくれるか?
一休は20年以上の歴史を持つサービスです。
継続的にモダナイゼーションを進めてはいるものの、まだまだレガシーコードが残っています。
そのようなレガシーコードを読んで理解することは、現状の振舞いや仕組み、そこに至った経緯を把握するために、避けて通れない作業です。
レガシーコード上でわからないことを GitHub Copilot Chat が適切に要約して回答してくれると、あちこち行ったり来たりすることなく、着目すべきコードに集中して読むことが可能になります。 ひいては開発生産性の向上にも寄与してくれるのではないか、と期待していました。
- 新しく入社した開発者がレガシーなリポジトリを見るとき、どこを読めばいいかを示してくれるか
- 営業スタッフやカスタマーサービスから問い合わせがあったとき、現状や経緯についてのピンポイントな質問に答えられるか
- リポジトリの全体感がどうだ、とかそういう質問に答えられるか
- もっと踏み込んで、検索にとどまらず改善策など示唆にあたる情報を提示してくれるか
具体的には上記のようなユースケースです。
このようなシナリオを評価するために、評価者が十分に理解しているような内容について、適切なまとめを返せるか、というテストを行いました。
このあたりは業務に深く関わってくる内容なので、具体例を紹介することは難しいのですが、たとえば、
複数のリポジトリを横断して内容をまとめる必要があるのですが、リポジトリ間でコードやコメントの質に差が大きく、より質の高いリポジトリに回答の内容が引っ張られてしまっている(ように見えた)
無関係の情報が回答に含まれないように、プロンプトの書き方や、knowledge bases にインデックスさせる情報を工夫する必要がある
XXX の API を呼びだしているところを探して、という質問で、関係のないプレゼンテーション層のコードを返してきたり、リポジトリのコードをあまり学習しているように感じられなかった
といった意見があり、期待した結果を得るにはハードルが高いなという印象でした。
もちろん、命名やコメントを含めてレガシーコード自体の品質に問題があることは否定できません。 ですが、そのようなコードベースであっても適切に情報を抽出できなければ、レガシーコードを扱う上での助けにはならないのが実情なのです。
PR メッセージ自動生成
Pull Requests のメッセージを自動で生成する機能は現状英語しかサポートされていません。
ソフトウェアエンジニアとして英語ドキュメントに触れる機会は多いといっても、社内コミュニケーションはもちろんのこと日本語です。 人に読んでもらうための PR メッセージが母語でなければ、当然、その効率は著しく下がってしまいます。 ノンバーバルな情報が得られない文章によるコミュニケーションにおいて、重要となる細かなニュアンスを伝えることも難しくなります。
また、英語であることを差し引いたとしても、生成される内容が現状ではそこまで有用とは言えませんでした。
たとえば、どのようなファイルにどのような変更をおこなったかという what の情報はうまく要約してくれます。 しかし、その PR の変更が必要となった背景や変更の意図といった why の情報は期待したほどには盛り込まれません。
レビューにあたって what は差分を見ればわかります。 ですが、その変更が適切かどうかを判断するために欲しい情報は why なのです。
もちろん why をコードのみから読み取るのは人間でも難しいので、コメントの形で補足する必要があります。 しかし、コメントを書いたとしても、コードの変更箇所に関する限定的な内容となってしまいがちで、そもそもの背景や目的を網羅するのは現実的に難しいところがあります。 結果、PR の説明として期待するほどの内容にはなりませんでした。
将来的には Issue や git の履歴を利用して、背景情報を補ってくれるようになることを期待しています。
総じて PR メッセージ自動生成は機能自体が発展途上であり、現時点で導入したとしてもそこまで大きな恩恵を受けられるわけではなさそうだという結論に至っています。
学習の対象が限定的
他にも評価の過程で以下のような声が挙がりました。
DB 定義書を開くのが手間なので聞けたら便利だと思ったが、Excel ファイルを読み取ることはできなかった。
回避策として Excel の DB 定義ファイルから markdown に変換して knowledge bases リポジトリに登録してみました。
自動生成された markdown という制限付きではあるものの、テーブル間の関係を学習できていないように思えます。 たとえば、ある機能に関連するテーブル定義の全体像を説明して、といった質問には適切な回答が得られませんでした。
ADRのリポジトリがあるので、これをインデックスして仕様を聞けたら便利だとおもったが、issueは対象外だったのでうまくいかず。。。
GitHub に蓄えられた情報は git リポジトリ以外にも Issues や Pull Requests, Wiki が存在します。
LLM にとって、もっとも学習しやすい対象であるテキスト情報の上、過去の経緯を追う上でも重要な情報が含まれています。
にも関わらず、Copilot の学習対象外であるため、これまで蓄積してきた情報にもとづく知見を抽出することはできませんでした。
近い将来の導入に向けて
上述した通り、残念ながら、現時点ではすぐに効果が得られるようなユースケースは見つかりませんでした。
ですが、日進月歩を文字通り体現している LLM の発展を見る限り GitHub Copilot Enterprise を導入する未来は近いとは考えています。
したがって、いざ導入するとなったとき、すぐに有効活用できるよう準備は進めておくのがよさそうです。
今回は採用を見送ったものの、評価内容を踏まえてコードとドキュメントの二つの観点で、どういった準備をしておくべきかの認識を共有して評価プロジェクトを終了しました。 といっても頑張って準備する類の活動ではなく、頭の片隅においておこう、という程度の対策です。
最後にその対策をご紹介して本記事を終えようと思います。
コードに意図が伝わるコメントを残す
自動生成された Pull Requests のメッセージは修正した内容の要約という what であって、その修正がどういう意図でなされたか、レビューにあたって特に重要な why は含まれていません。
もちろん、それはコードに意図や理由にあたる情報がないためであって、Copilot が why を説明するメッセージを生成できないのも当然です。
GitHub の Blog でも、Copilot を使う上でのベストプラクティスとして LLM に context を提供することの重要性を説いている記事が公開されています。
ということで、ごく当たり前の結論ではありますが、コード自体に why や why not がわかるコメントをしっかり残すように意識していこう、となりました。
奇しくも同時期に行っていた A Philosophy of Software Design の輪読会でコメントの重要性についての議論をしていたのも功を奏しました。 コードに意図が伝わるコメントを記述する、というプラクティスが各チームに浸透してきており、今後 LLM に与えられる context が増えていくと見込んでいます。
また、副次的な効果として、フロー情報になってしまいがちな PR と異なり、ストック情報と言えるコード上のコメントは認知負荷を軽減してくれています。 普段から触れるコードだけで意図が伝わる状態と比べたとき、なにかしら問題が起きてから git の履歴や関連する PR を追う作業は、不要な課題外在性負荷でしかありません。
なお、前段で PR メッセージ生成の評価の中でコメントを追加しても why を含んだ内容は生成されなかった、という評価結果をご紹介しました。 これは、あくまで現時点で未成熟なだけであって、将来に向けての布石としては、コメントを充実させていくことには意味があると捉えています。
今後はコメントに加えて、どうすれば LLM フレンドリーなコードになるか、という観点での新しいコードの書き方も確立していくでしょう。引き続き動向を追いながら、新しい種類のコードの品質向上に努めていきたいと思います。
ただ、このような新しいプラクティスが浸透するのには時間がかかります。 Copilot の今後の進化で、ブランチと紐付けた Issue や PR に代表される、コードに関わる既存の context をうまく利用してくれるのでは、と個人的には期待しています。
ドキュメントの準備はあえて何もしない
近い将来の導入に向けて、今からドキュメントを GitHub に移行していくことも検討しました。 しかし、現時点では、あえて何もしないことを選択しました。
GitHub Copilot Enterprise がナレッジマネジメントの分野においても、LLM 時代のスタンダードになるかどうかはまだ判断しきれなかったからです。
もちろん、コードそのものに加えて Issue や PR の情報を持っているという強みがあるので、非常に有力な候補であることには疑う余地はないでしょう。
ですが、今はどの会社も LLM を自社製品にどう組み込むか最優先で試行錯誤しているのは間違いなく、どの製品が最終的に勝者となるかは未知数です。 Google が後発の検索エンジンであったことを忘れてはなりません。
一休では、前述したように多くのチームでドキュメンテーションに Confluence を利用しています。 Atlassian でも Atlassian Intelligence という AI 拡張機能が提供されはじめています。 Confluence には AI を利用した要約や検索、社内用語やプロジェクト用語の自動定義などの魅力的な機能が近日中に提供されるようです。
GitHub もまた、knowledge bases を単にリポジトリ中の文書を学習するだけに留めず、Copilot の中核となる機能として発展させる施策を進めているのではないかと予想しています。 たとえば Issues や Discussions, Pull Requests など GitHub に蓄えられた他の情報との統合は容易に想像できるところです。
加えて、忘れてはいけない観点として、ナレッジマネジメントサービスにとって、既存機能の重要性には変化がないことには触れておきたいと思います。 LLM による新しい検索体験は非常に強力で魅力的なフィーチャーであることは確かです。 しかし、情報の構造化やチームでの同時編集のしやすさ、他サービスとの連携といった、もともとの価値を見失うことがないよう留意していくつもりです。
将来、他のナレッジマネジメントサービスを採用することになったとしても、knowledge bases リポジトリの準備でご紹介したようにデータ移行はさほど難しくはありません。加えて、この分野で高いシェアを持つ Confluence からの移行機能が提供されることも期待できます。
引き続き動向を注視しながら、あらためて判断することになりそうです。
おわりに
一休では、よりよい価値を素早くユーザーに提供できるよう、開発生産性の向上にもチャレンジしていただける仲間を募集しています。
興味を持っていただけたら、ぜひ一休の採用サイトをご覧ください。